Dimensional Analysis (also called Factor-Label Method or the Unit Factor Method) is a problem-solving method that uses the fact that any number or expression can be multiplied by one without changing its value. It is a useful technique.
Unit factors may be made from any two terms that describe the same or equivalent "amounts" of what we are interested in. For example, we know that
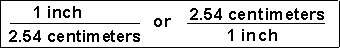
(1) How many centimeters are in 6.00 inches?
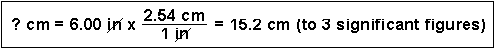
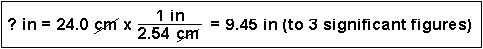
(3) How many seconds are in 2.0 years?
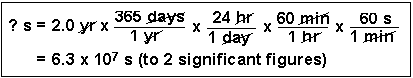
Scientists generally work in metric units. Common prefixes used are the following:
| Prefix | Abbreviation | Meaning | Example |
|---|---|---|---|
| mega- | M | 106 | 1 megameter (Mm) = 1 x 106 m |
| kilo- | k | 103 | 1 kilogram (kg) = 1 x 103 g |
| centi- | c | 10-2 | 1 centimeter (cm) = 1 x 10-2 m |
| milli- | m | 10-3 | 1 milligram (mg) = 1 x 10-3 g |
| micro- | 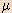 | 10-6 | 1 micrometer (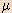 g) = 1 x 10-6 g) = 1 x 10-6 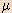 g g |
| nano- | n | 10-9 | 1 nanogram (ng) = 1 x 10-9 g |
(4) Convert 50.0 mL to liters. (This is a very common conversion.)
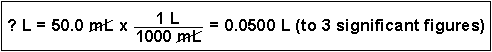
(5) What is the density of mercury (13.6 g/cm3) in units of kg/m3?
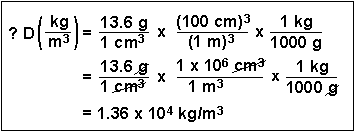
(6) How many atoms of hydrogen can be found in 45 g of ammonia, NH3?
We will need three unit factors to do this calculation, derived from the following information:
- 1 mole of NH3 has a mass of 17 grams.
- 1 mole of NH3 contains 6.02 x 1023 molecules of NH3.
- 1 molecule of NH3 has 3 atoms of hydrogen in it.
